LOGIC GATES/CIRCUITS 1 - DEFINITION, TYPES, SYMBOLS AND USES

 LOGIC GATES/CIRCUITS 1 

DEFINITION, TYPES, SYMBOLS AND USES

DEFINITION OF LOGIC GATE

A logic gate is the fundamental building block of digital integrated circuits. Most logic gate takes an input of two binary values, and output a single value of 1 or 0. Some circuits may have only a few logic gates, while others, such as microprocessors, may have millions of them. Logic gates are primarily implemented using diodes or transistors acting as electronic switches, but can also be constructed using vacuum tube, fluidic logic, optics, molecules or even mechanical elements.

Logic circuit includes such devices as registers, arithmetic logic units, and computer memory, all the way up through complete microprocessors, which may contain more than 100 million gates.  

Equation and truth table for each logic gate

The truth table is the table that shows the possible combinations of variable values in the equation and the result (output) for each of the logic gates.

For a two-input truth table, there will be 4 (2²) possible combinations of variable inputs and generally for n-input truth table, there will be 2ⁿ possible combinations of the input variables. See the examples below:

Types of logic circuit

There are mainly 5 logic gates, they are:

a        OR gate

b         AND gate

c         NOT gate

d. NAND Gate

e. NOR Gate

   a..  OR gate: 

The OR gate is a circuit that has two or more inputs and operates in such a way that:

·         Its output is 1 when any of the input variables is 1

·         Its output is 0 if when all of the input variables are 0

·         Its output is 1 when all of the input variables are 0

The algebraic symbol of the OR operation is the plus sign (+).

OR Gate Symbol

b         AND gate

The AND gate is a circuit that has two or more inputs and operates in such a way that:

·         Its output is 1 if and only if the two inputs are 1

·         Its output is 0 if any of the inputs is either 0 or 1 or both are 0

The algebraic symbol of the AND gate is * or .. The AND gate is represented graphically below.

         

The AND gate is represented in a truth table (with two inputs A and B) as shown below:

A	B	X=A * B
0	0	0
0	1	0
1	0	0
1	1	1

It can also be generated using the equation: X=A.B

c.         NOT gate

This is the logic gate that has one input and one output such that when the input is true (1), the output is false and when the input is false, the output is true.

The algebraic symbol of the NOT gate is     or ‘. The NOT gate is represented graphically below.

The truth table for the NOT gate (with input A): x= A’ or x= Ᾱ is shown below:

A	X = A’
0	1
1	0

d. NAND Gate

NAND GATE

This is a logic gate whose output is zero (0) if both of the inputs are 1and 1 otherwise. A NAND gate is equivalent to an AND gate followed by a NOT gate. The NAND gate is the complement of the AND function. The word NAND is got from the abbreviation NOT-AND. The NAND gate is represented graphically below.

The truth table is shown below

e. NOR GATE

The NOR gate out is the direct inverse of the OR gate output for all possible input conditions as can be seen from the truth table below. It is short for NOT OR.

The NOR gate works like an OR gate followed by an INVERTER so that circuits in the diagram below are equivalent.

          LOGIC GATES/CIRCUITS 2

TRUTH TABLE AND EQUATION FOR EACH LOGIC GATE

MEANING OF TRUTH TABLE

A truth table is a table/breakdown of all the possible truth values returned by a logical expression. A truth value is typically either true or false, or 1 or 0. It is a table that contains the lists of the value of the output for every combination of logic inputs.

Logic Equations

Aside from representing the function of a logic gate with a truth table and grammatical definition, the use of logic equations can be used to represent logic gates and circuits.
The AND gate Equation
The AND gate operation can be expressed by a Boolean algebra equation. For a 2-input AND gate, the equation is:
X=A.B
The symbol for the AND operation is a centre dot (.). It does not mean multiplication. The expression reads ‘X’ equal to A and B.
The OR Gate Equation
The OR gate operation can also be expressed by a Boolean algebra equation. For a 2-input OR gate, the equation is:
X= A+B
The symbol for the OR operation is a +. It does not mean addition. The expression reads X equal to A or B.
NOT Gate Equation
The NOT gate operation can also be expressed by a Boolean algebra equation
X= Ā
A complement bar (also called an over bar) is placed over the assigned input letter. The expression reads ‘X’ is equal to not ‘A’.

LOGIC GATES/CIRCUITS 3

ALTERNATIVE LOGIC GATES

DESCRIPTION AND TRUTH TABLE

DIGITAL COMPARATOR

A digital comparator is a very useful application of logic circuit.

A digital comparator is an electronic device that takes two numbers as input in binary form and determines whether one number is greater than, less than or equal to the other number. A comparator compares two input voltages and indicates which is higher. Comparators are used in central processing units (CPUs) and microcontrollers (MCUs).

Note: A XNOR gate is a basic comparator, because its output is "1" only if its two input bits are equal. The XNOR gate is graphically represented below:

A	B	X
0	0	1
0	1	0
1	0	0
1	1	1

          

                                                                   

         

The analog equivalent of digital comparator is the voltage comparator. Many microcontrollers have analog comparators on some of their inputs that can be read or trigger an interrupt

Construction of a simple comparator using XOR

One of the special logic circuit that occurs quite often in digital system is the exclusive-OR (XOR) circuits.

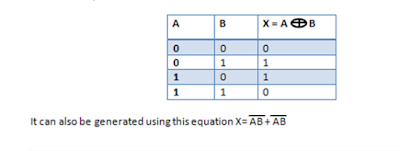
The XOR produces a high voltage only when the two inputs are at opposite levels. This means that the XOR yields true (1) if and only if one of the inputs is true (1) and the other is false (0). The XOR gate is graphically represented below.

               

The XOR is represented in the truth table below

Uses of Logic Gates

Logic gates are widely used in various applications such as:

1.           Electronics: Logic gates are the building blocks of digital electronics, they are formed by combining transistors to realize some digital operations. Every digital product such as computers, mobile phones contain logic gates

2.           Decision making:  The term logic is usually used to refer to a decision making process. A logic gate can give a yes or no response based on the input it receives

3.           Alarms: Logic gates are used to construct alarms used in cars and homes. Pressing the alarm button gives an output of 1. When the bell is released, on output of 0 is recorded